Et primtal er et helt tal større end 1, der ikke er deleligt med andre hele positive tal end 1 og tallet selv. De første primtal er 2, 3, 5, 7, 11, ... . Da ethvert helt tal entydigt kan skrives som et produkt af primtal (se primfaktor), kan primtallene opfattes som de multiplikative byggesten for de naturlige tal. Et helt, positivt tal, der ikke er et primtal, kaldes sammensat.
Faktaboks
- Etymologi
- 1. led i ordet primtal kommer af latin primus 'første'.
Primtallene har lige siden oldtiden været genstand for matematikeres interesse. Euklid viste således, at der findes uendelig mange primtal, og Eratosthenes angav en metode til bestemmelse af samtlige primtal (Eratosthenes' si).
Primtal spiller en stor rolle i talteori, og især store primtal har vist sig at have vigtige anvendelser inden for bl.a. kodningsteori og kryptologi. Det største kendte primtal (2016) er 274.207.281-1, der skrevet i titalssystemet har flere end 22 mio. cifre.
Ved metoder fra den analytiske talteori viste P.L. Dirichlet, at enhver differensrække a,a+d,a+2d, ... indeholder uendelig mange primtal, såfremt a og d er indbyrdes primiske hele tal. Det er et berømt uløst problem, om der findes uendelig mange primtalstvillinger (tal a og a+2, der begge er primtal).
Et ofte rejst, lidt upræcist spørgsmål er, om der findes en "formel" for det n'te primtal. Hvis man kender primtallene på forhånd, kan man konstruere en formel, men sådanne formler er uden praktisk interesse. L. Euler fandt i 1772 polynomiet x2−x+41, der for alle 80 heltallige værdier af x mellem −39 og 40 giver et primtal. Det kan imidlertid vises, at der ikke findes et polynomium i én variabel med heltalskoefficienter, der for alle heltallige værdier af den variable giver et primtal. Et interessant resultat er, at der findes et polynomium f (x1, ... ,x26) i 26 variable med heltalskoefficienter med den egenskab, at et naturligt tal h er et primtal, netop når der findes hele, ikke-negative tal h1, ... ,h26, så h = f (h1, ... ,h26).



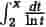
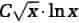

Kommentarer
Kommentarer til artiklen bliver synlige for alle. Undlad at skrive følsomme oplysninger, for eksempel sundhedsoplysninger. Fagansvarlig eller redaktør svarer, når de kan.
Du skal være logget ind for at kommentere.